Ⅰ. 介紹
GTWR
GTWR (Geographically and Temporally Weighted Regression) 地理時間加權回歸,屬於 GWR 的擴展版本,為地理資訊科學(GIS)中探討空間數據關係的統計方法。
GTWR 不僅考量地理位置對於反應變數的影響,也考量到時間因素,並能同時處理空間和時間的變異性,例如疾病傳播、房地產市場波動等,而這些模式都可能因時間和空間的不同而有所改變。
主要特點與考慮因素:
1.空間和時間的權重:使用地理和時間加權來計算每個位置和時間點的迴歸參數。其意味相對近的觀測值(無論在空間或時間上)對該點的迴歸參數影響越大。
2.模型解釋:GTWR 與 GWR 類似,均能生成參數地圖,顯示某一特定參數如何隨地理位置和時間而變化,利於解釋空間變異性。
3.數據需求:考量 GTWR 模型的複雜性,它需要大量數據來確保結果的穩定性和可靠性。同時,數據應涵蓋充足的時間及空間範疇,以便正確估計模型參數。
4.計算量高:GTWR 需要更多的計算資源,因為它在每個地理位置和時間點都有一個迴歸方程式。
Plugin 優點
1.操作簡單
使用者僅需安裝 R 及 QGIS ,在QGIS中安裝 Processing R Provider 插件後,再將相關程式文檔複製到指定路徑下即可使用。若後續需進行任何更改或調整,可直接更改程式文檔。
2.時間分組
使用者可根據需求將資料中的時間變數進行分組,不論是每日、每月、每年或期數等,皆能進行分組,例如將每五天分為一組,作為新的時間變數,或將每日資料合併成每月等,使用者可以調整所需的單位(年、月、日或預設資料單位),以及區間。選擇完後,GTWR 模型會使用新建立的時間分組作爲時間變數。
※若原本資料時間變數尺度較大,例如年或月,則選擇單位無法選擇更小的單位例如月或日,假設資料為期數等非日期格式,單位僅能選擇預設資料單位。
3.模型視覺化
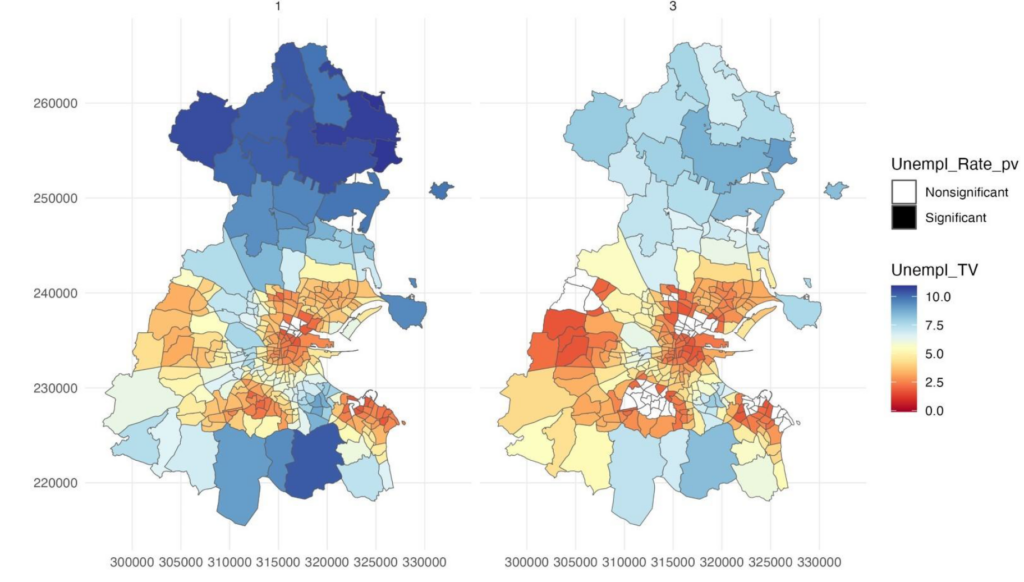
執行程序後,在使用者所指定的資料夾會新增各解釋變數當中,各個地點以及時間的 T 值結果視覺化圖片,其中若該地點在這解釋變數有顯著的話則會根據T值大小顯示不同顏色,若不顯著則會是白色。
4.QGIS 縮減變數名稱問題
QGIS 在處理資料時會將超過十個字元的變數名稱進行縮減,而在參數選單則仍為原本完整的變數名稱,因此在這個程序也會依照 QGIS 的方式對於使用者所選變數名稱進行縮減,避免 QGIS 後端資料的變數和使用者所所選不同所導致的問題。不過由於 QGIS 縮減名稱方式和變數順序有關,因此若使用者所選的變數順序和原先資料的變數順序不同則仍會出現問題。
Ⅱ. 安裝流程 (For Mac User)
Step 1
安裝QGIS & R
Step 2
開啟QGIS後於上方欄位點選「Plugins」 > 「Manage and install Plugins」
Step 3
搜尋「Processing R Provider」後 ,點選 「Install Plugin」 > 「關閉」
Step 4
重啟QGIS後,於上方欄位點選「Setting」 > 「Options」
Step 5
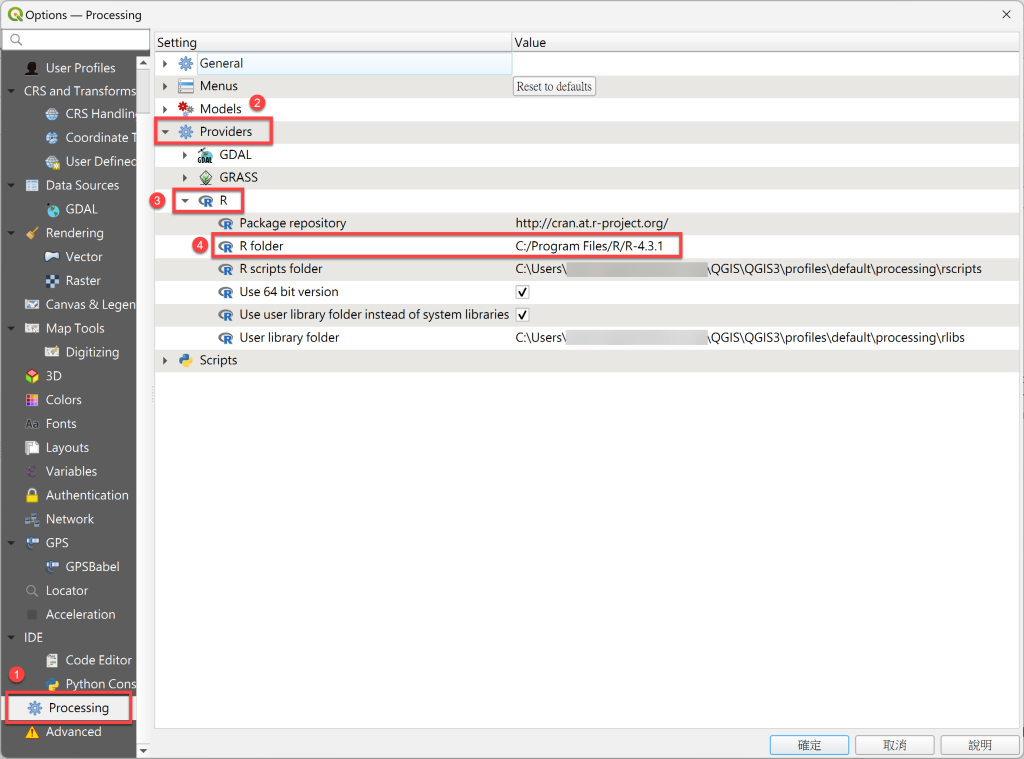
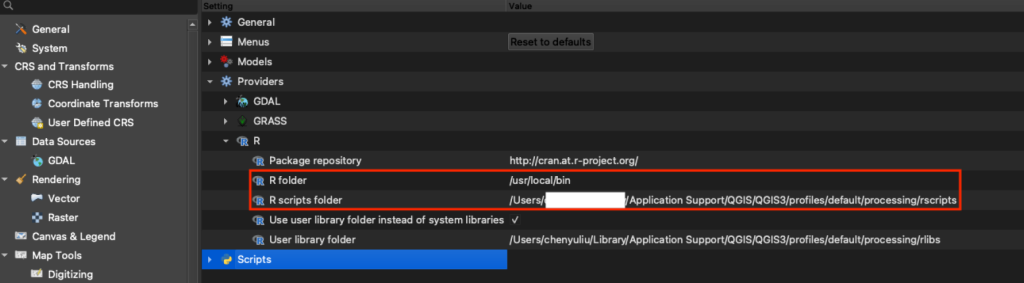
點選「Processing」 >「 Providers」 > 「R」,設定R folder 路徑(例如:C:\Program Files\R\R-4.3.1,實際路徑可能因系統、版本或是路徑而異)
※若R安裝版本為 64 bit ,須將「Use 64 bit version」勾選
Step 6
開啟「R scripts folder」資料夾。
※此資料夾用於存放 gwr 或其他 R 程式檔案(路徑是在 QGIS 的安裝目錄下)。
Step 7
R scripts folder 資料夾下增加 gtwr.rsx、gtwr.help 程式檔

Step 8
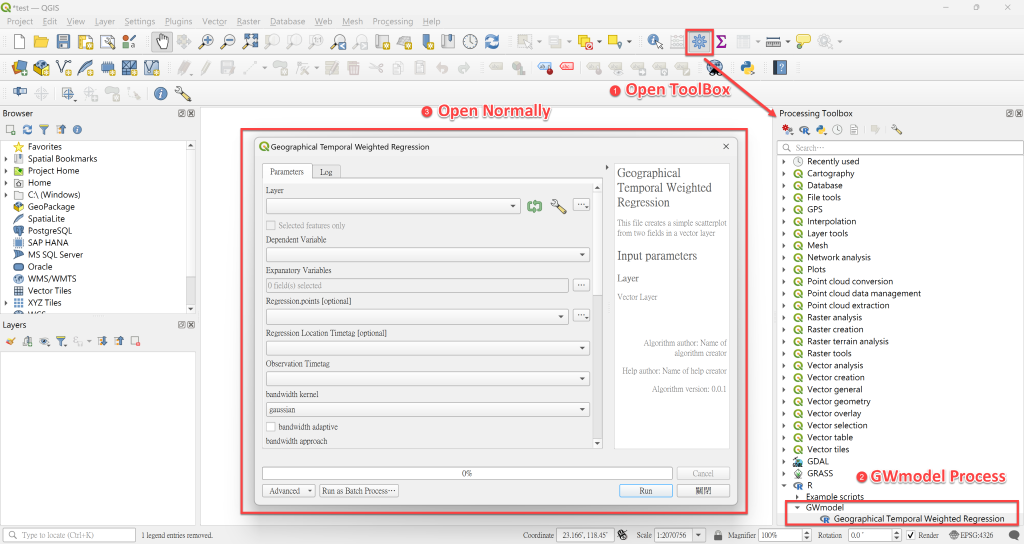
重啟QGIS,於 Processing ToolBox 確認是否成功安裝R類別及其下的 GWmodel 資料夾。若在 GWmodel 類別中看到 Geographical and Temporal Weighted Regression 程序,並能正常開啟,則表示已安裝完成。
※出現 Geographical and Temporal Weighted Regression 程序,但開啟出現問題,則可能為 Step 2 的 R folder 路經出現問題。
Ⅲ. 範例操作
Step 1 輸入資料
● 匯入時空點資料或時空面資料。
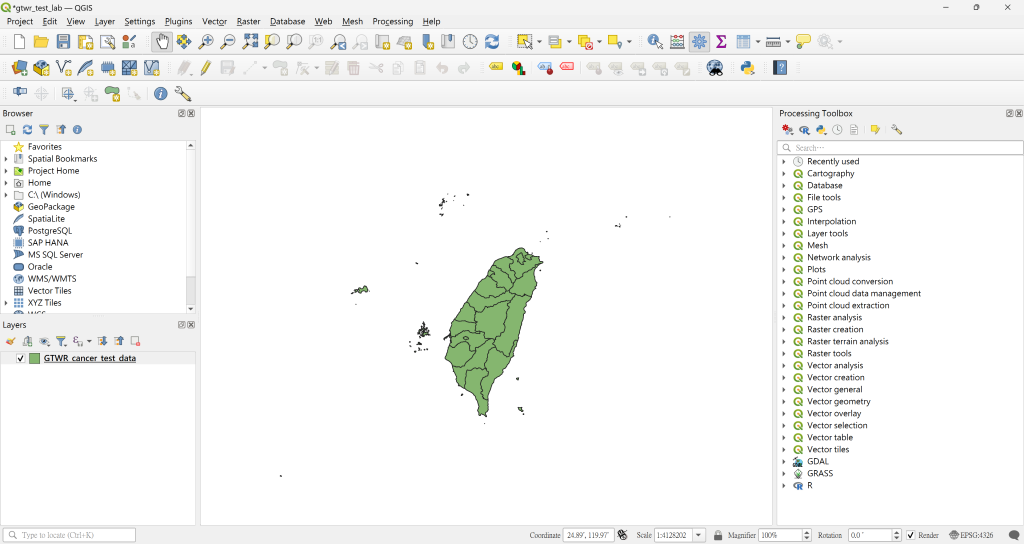
● 匯入資料後,開啟 Geographical Temporal Weighted Regression 程序,於 Layer 選取輸入資料。

Step 2 選擇參數
此部分為使用者主要操作介面,可根據需求選擇相對應的參數和輸入,並定義輸出資料路徑。
● 反應變數
所有變數單選選單,可依需求選擇相應的反應變數。

● 解釋變數
所有變數多選選單,可依需求選擇相應的解釋變數。

● 時間變數
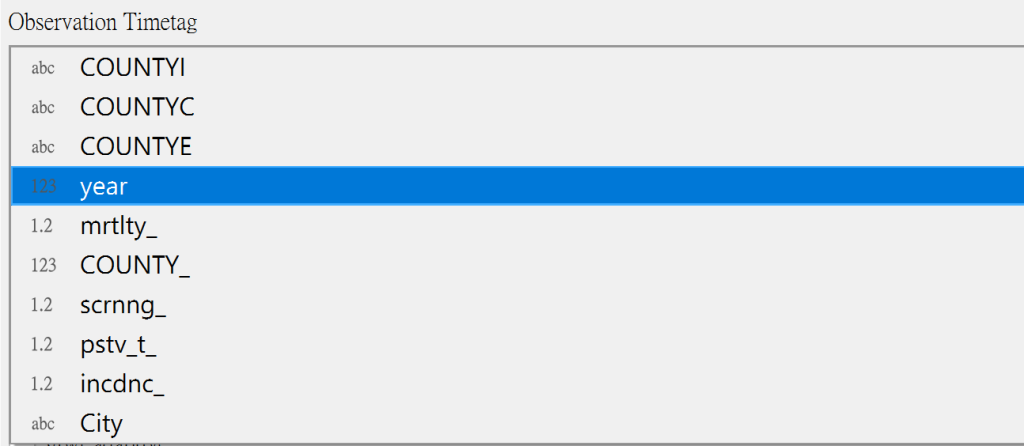
● Kernel、Approach 以及Fixed / Adaptive 選擇
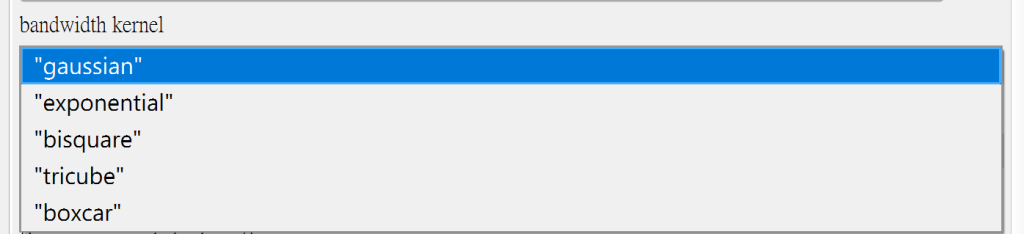
選擇計算 Bandwidth 的參數及後續模型的參數。
○ Kernel Funciton – Gaussian、Exponential、Bisquare、Tricube、Boxcar
○ GTWR Approach – CV、AIC、AICc、BIC

○ Fixed or Adaptive bandwidth

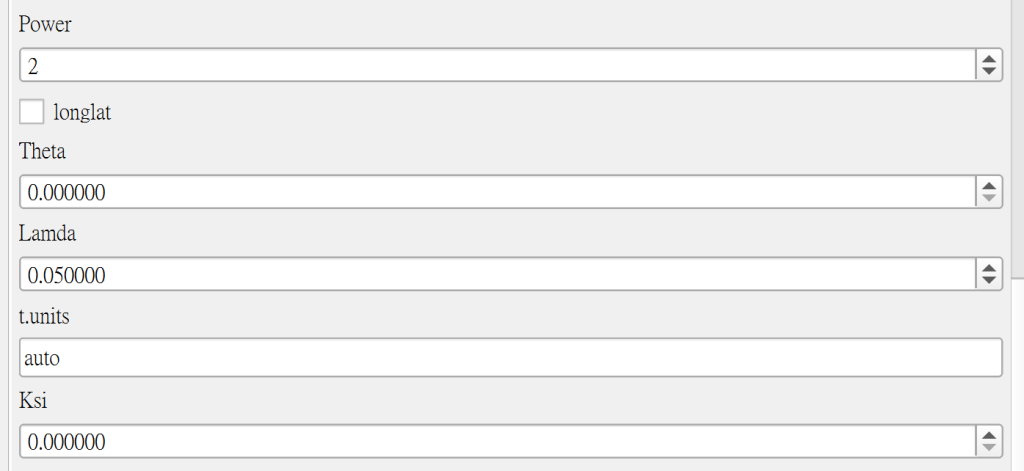
● 其他參數選擇
皆有預設值,可以根據情況自行調整。
● 輸出資料路徑
需指定資料輸出路徑

Step 3 日期分群
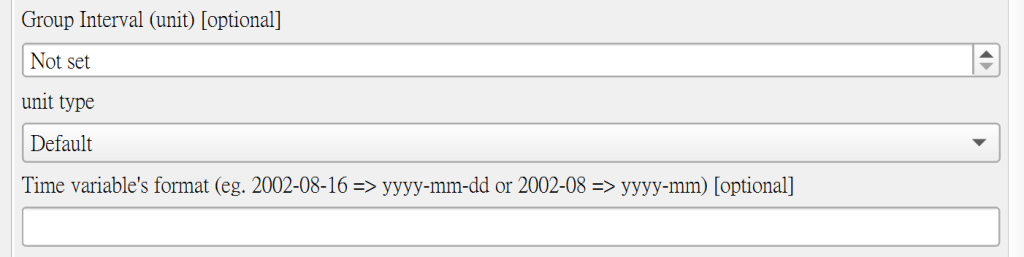
● 可選擇是否將目前的時間變數進行分群,例如每五天為新的一組或是將每月資料合併成每年、每日資料合併成每月等等。不論資料型態是日期或是期數等等都可以根據需求進行分組。進行分組後,模型會使用新的分組時間變數進行建模。
● 使用者需要先選擇區間大小以及單位,需要注意單位僅能選擇比時間變數尺度更大的,例如時間變數為每日,則單位可以選擇任一種,若時間變數為每月則無法選擇尺度更小的每日,以此類推。若時間變數並非日期格式,例如期數等等,則單位選擇 Default 即可。若是時間變數為日期,則需要特別輸入日期格式。


Step 4 輸出結果
● 文檔輸出
在QGIS執行程序的過程中,主要會輸出兩部份資料:
1. 不同 Bandwidth 的分數:由於在參數中選擇 Fixed 的 Bandwidth 以及透過 CV 的分數去進行選擇,因此輸出結果會有不同的 Bandwidth 及其對應的分數 ( 參見左下圖 )。
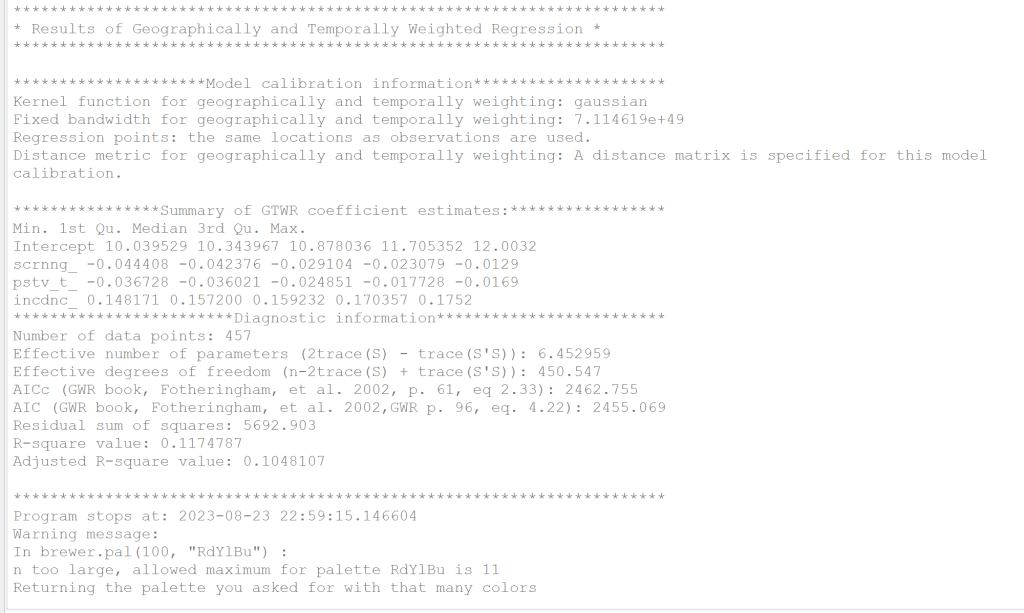
2. 模型的結果:可以看到模型的基本資訊,例如 AIC、AICc、R Squared 等,還有各係數的最大最小值等( 參見右下圖 ),此內容會同時輸出為一個文檔到使用者所設定的輸出路徑中。

● 資料輸出
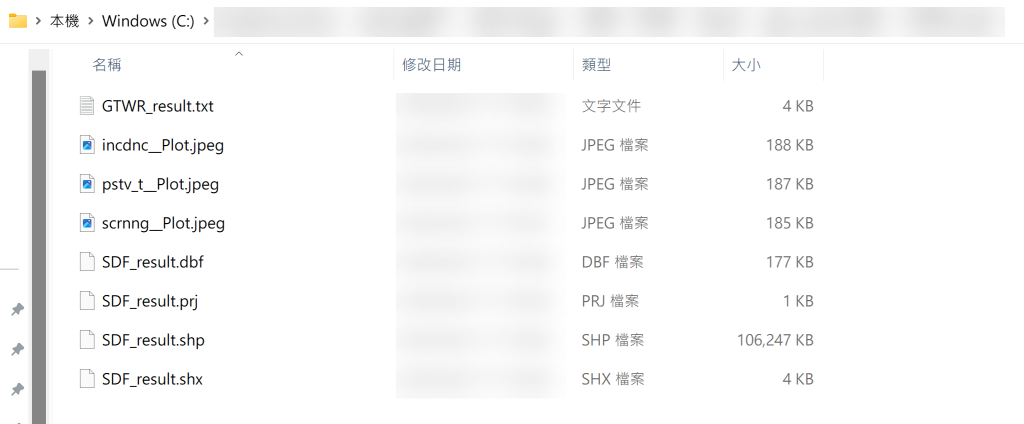
執行程序完畢,會在使用者指定的路徑中建立「 GTWR_result 」的資料夾 ( 參見左下圖 ),該資料夾共有三大部分內容:
1. 「 GTWR_result.txt 」:模型的資訊文檔 ( 參見右下圖 )。
2. 模型輸出結果 Shapefile:包含 「 SDF_reuslt.shp 」、「 SDF_result.shx 」、「 SDF_result.dbf 」以及「SDF_result.prj 」四個檔案,使用者若要使用,可將 SDF_result.shp 檔案輸入 QGIS 中 ( 參見右下圖 )。程序完成後 QGIS 會新增一個圖層 Output ,與 SDF_result.shp 檔案內容相同,皆為模型輸出結果。

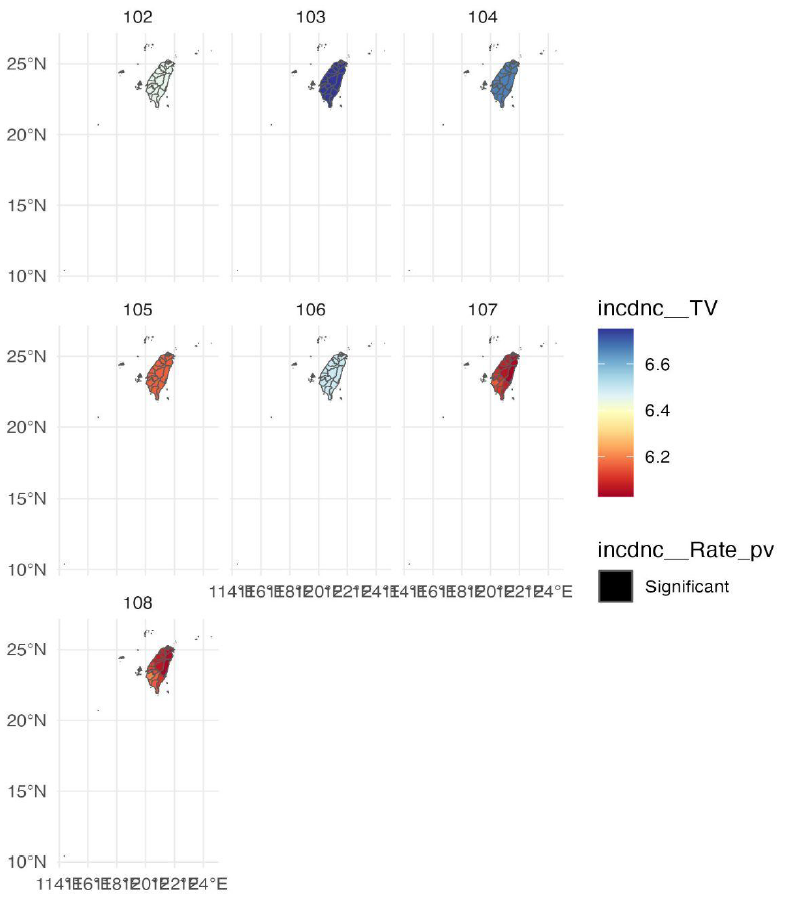
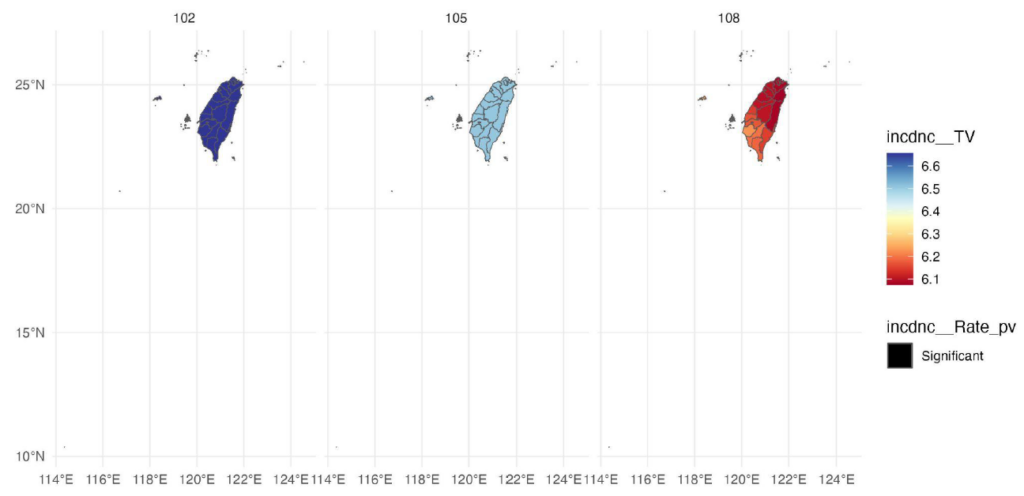
3. 模型各個解釋變數 T-value 在各個時間點視覺化結果:其中若是該地區或點的檢定結果為不顯著,則不會有任何顏色呈現,反之若是顯著,則會根據數值大小有有不同的顏色和深淺。同時若使用者有進行時間的分組,則視覺化結果的時間點會有所不同。左下圖為未進行時間分組視覺化結果,右下圖則為三年一組視覺化結果。
想了解更多,可參考以下資料:
[1] Chan, T. C., Chiang, P. H., Su, M. D., Wang, H. W., & Liu, M. S. Y. (2014). Geographic disparity in chronic obstructive pulmonary disease (COPD) mortality rates among the Taiwan population. PloS one, 9(5), e98170.
[2] Fotheringham, A. S., Crespo, R., & Yao, J. (2015). Geographical and temporal weighted regression (GTWR). Geographical Analysis, 47(4), 431-452.
[3] Nugroho, W. H., & Sumarminingsih, E. (2021, March). Geographically and Temporally Weighted Regression Model with Gaussian Kernel Weighted Function and Bisquare Kernel Weighted Function. In IOP Conference Series: Materials Science and Engineering (Vol. 1115, No. 1, p. 012063). IOP Publishing.
[4] Wu, B., Li, R., & Huang, B. (2014). A geographically and temporally weighted autoregressive model with application to housing prices. International Journal of Geographical Information Science, 28(5), 1186-1204.
 需下載軟體 – QGIS & R
需下載軟體 – QGIS & R